অবিন্যস্ত উপাত্ত : পূর্বে বর্ণিত শিক্ষার্থীদের গণিতে প্রাপ্ত নম্বরগুলো হলো অবিন্যস্ত উপাত্ত। এখানে নম্বরগুলো এলোমেলোভাবে আছে। নম্বরগুলো মানের কোনো ক্রমে সাজানো নেই।
বিন্যস্ত উপাত্ত: উপরে বর্ণিত নম্বরগুলো মানের ঊর্ধ্বক্রম অনুসারে সাজালে আমরা পাই,
৫০, ৫৫, ৬০, ৬০, ৬০, ৬০, ৬৫, ৬৫, ৬৫, ৬৫, ৭০, ৭০, ৭০, ৭৫, ৭৫, ৭৫, ৭৫, ৮০, ৮০, ৮৫, ৮৫, ৮৫,৮৫, ৮৫, ৯০, ৯০, ৯০, ৯০, ৯৫, ৯৫, ৯৫, ৯৫, ৯৮, ৯৮, ১০০।
এভাবে সাজানো উপাত্তসমূহকে বিন্যস্ত উপাত্ত বলে।
অবিন্যস্ত উপাত্তকে বিন্যস্ত করার সহজ নিয়ম
উপরে বর্ণিত প্রাপ্ত সর্বনিম্ন নম্বর ৫০ এবং সর্বোচ্চ নম্বর ১০০। এখানে নম্বরের ব্যপ্তি হলো (১০০-৫০)।
এখন শ্রেণিবিন্যাস করার জন্য ৫০ বা ৫০ এর কম সুবিধাজনক যেকোনো একটি সংখ্যা ধরা যায়। এখানে ৪৬ থেকে শুরু করে প্রতি ৫ নম্বরের ব্যবধানে শ্রেণিবিন্যাস গঠন করা হয়েছে। এক্ষেত্রে শ্রেণিব্যাপ্তি ৫। উপাত্তের সংখ্যার উপর ভিত্তি করে সুবিধাজনক ব্যবধান নিয়ে উপাত্তগুলোকে কতগুলো শ্রেণিতে সাধারণত বিভক্ত করার প্রক্রিয়াই শ্রেণিবিন্যাস।
উপাত্তের সংখ্যার ভিত্তি করে শ্রেণি ব্যবধান সাধারণত সর্বনিম্ন ৫ ও সর্বোচ্চ ১৫ নির্ধারণ করা হয়। শ্রেণিবিন্যাস শ্রেণির সংখ্যা অর্থ্যাৎ সংখ্যা শ্রেণি নির্ধারণের জন্য নিচে সূত্র ব্যবহার করা হয়।
পরিসর = (বৃহত্তম সংখ্যা ক্ষুদ্রতম সংখ্যা) + ১
উপাত্তের শ্রেণিসংখ্যা = (বৃহত্তম সংখ্যা- ক্ষুদ্রতম সংখ্যা) + ১ / শ্রেণিব্যপ্তি
বা =১০.২ = ১১ ।
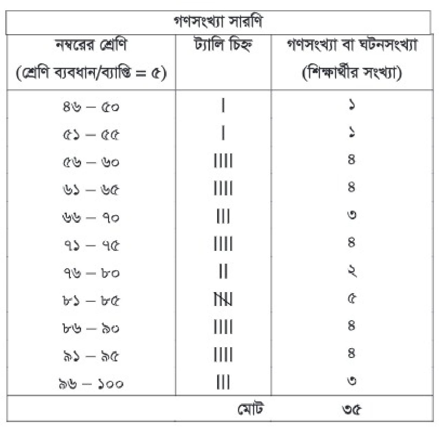
শ্রেণিসংখ্যা দশমিক ভগ্নাংশ হলে পরবর্তী পূর্ণ সংখ্যাটিকে শ্রেণিসংখ্যা হিসেবে বিবেচনা করা হয়। সুতরাং ৪৬ থেকে আরম্ভ করে শ্রেণিব্যাপ্তি ৫ ধরে শ্রেণিবিন্যাস তৈরি করলে শ্রেণিসংখ্যা হবে ১১টি। প্রথমে বামপাশে একটি কলামে নম্বরসমূহের শ্রেণিগুলো লিখতে হবে। এরপর প্রাপ্ত নম্বরগুলো একে একে বিবেচনা করে এবং প্রথম নম্বর যে শ্রেণিতে পড়বে তার জন্য ঐ শ্রেণির ডানে আর একটি কলামে ট্যালি (Tally) চিহ্ন'।' দিই। কোনো শ্রেণিতে যদি চারের বেশি ট্যালি চিহ্ন পড়ে তবে পঞ্চম ট্যালিচিহ্নটি চারটি চিহ্ন জুড়ে আড়াআড়িভাবে দিতে হয়। এভাবে শ্রেণিবিন্যাস শেষ হলে ট্যালিচিহ্ন গণনা করে শ্রেণি অনুযায়ী গণসংখ্যা বা ঘটন সংখ্যা নির্ধারণ করা হয়। এক্ষেত্রে কোনো শ্রেণিতে যতজন ছাত্র অন্তর্ভুক্ত হয়েছে তাই হলো ঐ শ্রেণির ঘটনসংখ্যা বা গণসংখ্যা। গণসংখ্যা সংবলিত সারণিই গণসংখ্যা সারণি। উপরের আলোচনায় বর্ণিত অবিন্যস্ত উপাত্তকে বিন্যস্ত করার গণসংখ্যা:
উদাহরণ ১। কোনো শহরের জানুয়ারি মাসের ৩১ দিনের তাপমাত্রা (ডিগ্রি সেলসিয়াস) নিচে দেওয়া হলো। গণসংখ্যা সারণি তৈরি কর (তাপমাত্রাগুলো পূর্ণসংখ্যায়)।
২০, ১৮, ১৪, ২১, ১১, ১৪, ১২, ১০, ১৫, ১৮, ১২, ১৪, ১৬, ১৫, ১২, ১৪, ১৮, ২০, ২২, ৯, ১১, ১০, ১৪, ১২, ১৮, ২০, ২২, ১৪, ২৫, ২০, ১০।
সমাধান: এখানে তাপমাত্রা নির্দেশক সংখ্যাগুলোর মধ্যে ক্ষুদ্রতম সংখ্যা ৯ এবং বৃহত্তম সংখ্যা ২৫।
সুতরাং প্রদত্ত উপাত্তের পরিসর (২৫৯) + ১ = ১৭। সুতরাং শ্রেণি ব্যপ্তি ৫ এর জন্য শ্রেণিসংখ্যা
∴ শ্রেণিসংখ্যা হবে ৪।
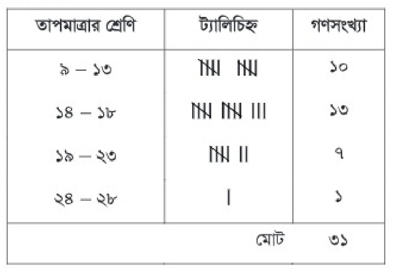
প্রদত্ত উপাত্তের গণসংখ্যা সারণি হলো
| কাজ: ১। একটি শ্রেণির ৩০জন করে শিক্ষার্থী নিয়ে এক একটি দল গঠন কর। প্রত্যেক দলের সদস্যদের উচ্চতা (সেন্টিমিটারে) পরিমাপ কর। প্রাপ্ত উপাত্তের গণসংখ্যা সারণি তৈরি কর। |
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
